Gradient Isochrones

An isochrone is a geographic area representing the set of locations one can reach from a given starting point by a given mode within a given amount of time. Isochrones are used extensively for measuring the quantity and quality of access a transport network provides, and we've written here about using them to measure playground access and job access.

But a devilish detail of PT isochrones, one absent in walking, cycling, and driving isochrones, is that they depend on PT schedules. Thus they and their corresponding access measurements are highly sensitive to departure time. (Another devilish detail, pertaining to any mode, is that the shape of the isochrone ---buffered streets vs. concave hulls vs. grid cell unions--- is a design choice. We'll address that detail in another post.)

For example, if your bus to work takes 12 minutes and departs near your home every half hour on the hour, then the 30-minute PT isochrone about your home with an 08:00 departure time will include your workplace, whereas the one with an 08:01 departure time will not, because getting to work starting at 08:01 takes 41 minutes by PT (29 minutes waiting for the next bus and 12 minutes riding it). How to capture that isochrone variation?

One method we use, which we call gradient isochrones, works as follows. Given an origin point and an isochrone time bound, we first choose a departure time window timely enough to capture most PT riders' departures to work, say, and big enough to capture the variety of PT service schedules operating near the origin, e.g. the weekday 08:00--08:35 time window. Then for each departure time in the window, at minute-ly spacing, say, we compute the PT isochrone from the origin at that time. Finally, we collect all the isochrones and overlay them, lightly colouring each. We used this approach in our review of Hawkes Bay's PT network plan.

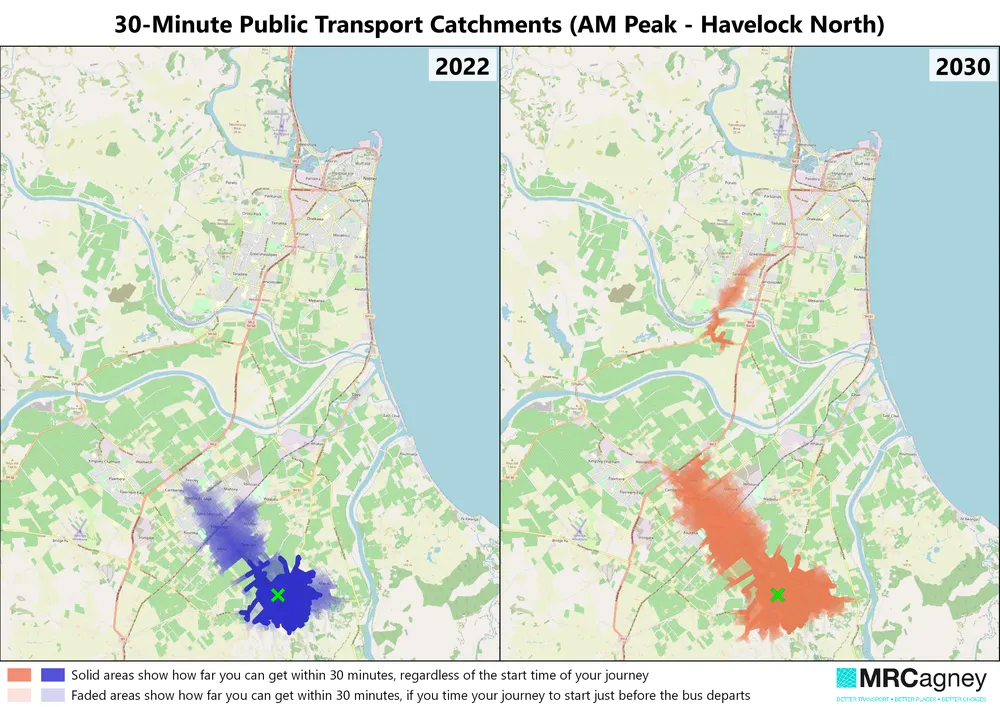
The gradient isochrones above show that people can easily access all of the Havelock North township within a 30-minute walk/PT journey in the 2022 PT network. But to reach most of Hastings, they must carefully time their journey starts, as indicated by the areas of light shading (little overlay). Contrast that with the 2030 network, in which people can access most of Hastings within 30 minutes, and if they time their journey well, they can get as far as Taradale.

"The gradient isochrone maps solve the challenge of how to visualize the temporal variation of access with public transport. They show at a glance what would take me ten minutes to explain and are invaluable to any network planning work I do." ~Lewis Thorwaldson, Senior Public Transport Planner at MRCagney

One drawback of gradient isochrones, however, is that the maps get hard to read when showing several origin points at once. More on tackling that issue in a future post.